این فصل به اجتماع مجموعه ها و اشتراک مجموعه ها اختصاص دارد. اجتماع دو مجموعه دلخواه A و B، مجموعه ای است شامل اعضایی که در یکی از این دو یا در هر دو مجموعه حضور دارد درحالی که اشتراک دو مجموعه A و B، مجموعه ای است تنها شامل اعضای مشترک دو مجموعه.

1-23 اجتماع

همانطور که در مقدمه اجتماع را تعریف کردم؛ هر عضو مجموعه اجتماع، حداقل در یکی از دو مجموعه حضور دارد. اجتماع دو مجموعه A و B را با نماد زیر بیان می کنیم:

(1)

$\large A \cup B $

اهمیتی ندارد که A و B کدام طرف علامت اجتماع باشند؛ چون هردو یک مفهوم را بیان می کند:

(2)

$\large A \cup B = B \cup A $

اجتماع A و B در نمودار ون، منحنی است که تمامی اعضای A و B، چه مشترک و چه غیرمشترک را در برمی گیرد؛ فرض کنید مجموعه های ما به صورت زیر باشند:

$\large A=\left \{ 1,2,3,4 \right \} , B=\left \{ 3,4,5 \right \}$

مطابق تعریف اجتماع، اجتماع دو مجموعه A و B به صورت زیر است:

$\large A \cup B = \left \{ 1,2,3,4,5 \right \} $

نمایش این دو مجموعه و مجموعه اجتماع آن ها به وسیله نمودار ون نیز امکان پذیر است:

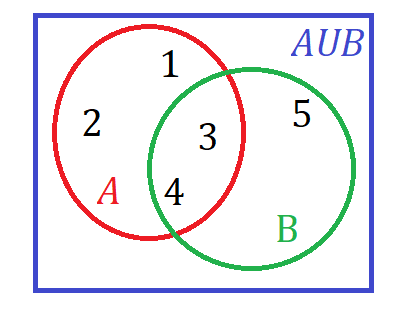
شکل 23-1، نمودار ون دو مجموعه و اجتماع آن دو

2-23 اشتراک

تنها اعضای مشترک دو مجموعه به اشتراک راه می یابند. قرینه نماد اجتماع، نماد اشتراک است و اشتراک دو مجموعه دلخواه A و B را به صورت زیر نشان می دهند:

(3)

$\large A \cap B $

به مانند اجتماع، اشتراک نیز جابجایی پذیر است:

(4)

$\large A \cap B = B \cap A $

دو مجموعه A و B که کمی بالاتر تعریف کردم، اشتراک آنها را به صورت زیر خواهد بود:

$\large A \cap B = \left \{ 3,4 \right \} $

در نمودار ون بخش نارنجی رنگ، اشتراک دو مجموعه موردنظر ماست:

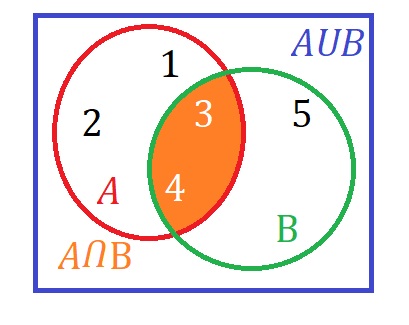
شکل 23-2، نمودار ون دو مجموعه و اجتماع و اشتراک آن دو

3-23 نکات اجتماع و اشتراک

اولین نکته این است که برای اجتماع گرفتن یا اشتراک گرفتن از چند مجموعه، اهمیتی ندارد از کجا شروع کنید، مثلا می خواهیم اجتماع سه مجموعه A و B و C را بیابیم. فرقی نمی کند اول A و B را اجتماع بگیریم، سپس اجتماع حاصل را با C اجتماع بگیریم یا اینکه اول A و C را اجتماع بگیریم سپس اجتماع حاصل را با B اجتماع بگیریم. اگر توضیحی که دادم کمی پیچیده بود، رسم نمودار ون این را برایتان روشن خواهد کرد. نتیجه اخلاقی این بند به صورت زیر است :

(5)

$\large (A\cup B)\cup C=(A\cup C)\cup B=(B\cup C)\cup A$

$\large (A\cap B)\cap C=(A\cap C)\cap B=(B\cap C)\cap A$

دومین نکته اینکه اشتراک همیشه زیرمجموعه اجتماع است:

(6)

$\large A\cap B\subseteq A\cup B $

نکته سوم اینکه اگر دو مجموعه دلخواه A و B هیچ عضو مشترکی نداشته باشند؛ اشتراک آنها مجموعه تهی است.

نکته چهارم اینکه اجتماع یک مجموعه دلخواه با تهی، خود مجموعه است و اشتراک یک مجموعه دلخواه با تهی، تهی است.

(7)

$\large A \cup \varnothing = A , A\cap \varnothing=\varnothing$

و اما پنجمین نکته! اگر اجتماع A و B با اشتراک A و B یکسان بود. A و B هر دو یک مجموعه اند (از جمله دوم نیز می توان جمله اول را نتیجه گرفت):

(8)

$\large A\cup B=A\cap B \Leftrightarrow A=B$

4-23 جمع بندی فصل

با اجتماع و اشتراک آشنا شدیم و چند نکته ساده اما کاربردی را باهم یاد گرفتیم. از این دو مفهوم، می توانیم مفاهیم جدید و دیگری نیز بسازیم. پس منتظر بمانید!

*1- به دو مجموعه که هیچ عضو مشترکی با یکدیگر نداشته باشند؛ دو مجموعه جدا از هم گوییم. تعداد اعضای اجتماع دو مجموعه جدا از هم چه ارتباطی با تعداد اعضای هریک از مجموعه ها دارد؟

*2- درستی گزاره زیر را برای یک مجموعه دلخواه چهار عضوی و زیرمجموعه سه عضوی اش بررسی کنید.

(9)

$\large A\subseteq B\Leftrightarrow A\cap B=A \; ,\; A\cup B=B$