در این فصل به تفاضل مجموعه ها می پردازیم. تفاضل دو مجموعه دلخواه A و B، به صورت A-B به این معنی است که اعضایی از A مدنظر ماست که در B نباشد. راستش قبلا نیز با این مجموعه کار کرده اید؛ در بازی اسم فامیل! اعضای این مجموعه بیشترین امتیاز را برای بازیکن به همراه می آورند چون مشترک نیستند.

1-24 تعریف

برای دو مجموعه دلخواه A و B، محموعه A-B شامل اعضایی از A است که در B عضو نیستند و مجموعه B-A شامل اعضایی از B است که در A عضو نیستند. می توان مجموعه A-B را به روش زیر نشان داد:

(1)

$\large A-B=\{x|x\in A , x \notin B\} $

نمایش نمودار ون نیز خالی از لطف نیست. اشتراک A و B از A حذف می شود:

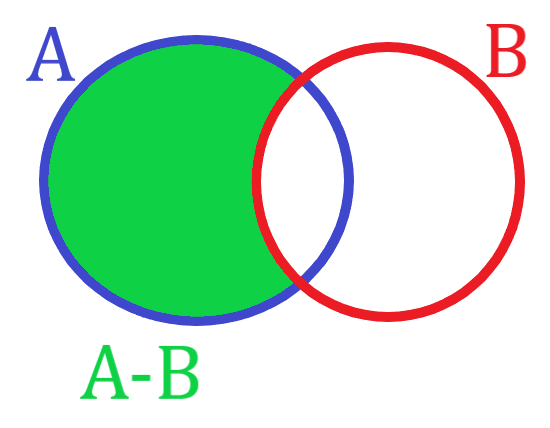
شکل 24-1، بخش سبز رنگ نشان دهنده A منهای B است.

* مثال 24-1)

مجموعه $A-B$ را برای $A=\{1,2,3,6\}$ و $B=\{8,-1,1,4\}$ تشکیل دهید.

پاسخ

برای این کار تنها کافی است اعضای مشترک A و B را از A حذف کنیم:

$\large A \cap B = \{1\} $

$\large A-B=\{2,3,6\} $

2-24 جمع بندی فصل

با تفاضل مجموعه ها آشنا شدیم. حال می توانیم به راحتی در بازی اسم فامیل، کلمات 20 امتیازی را تشخیص دهیم (اگرچه پیش از آشنایی با این مبحث هم مشکلی پیش نمی آمد!) تفاضل مجموعه ها یک بیان با اشتراک نیز دارد که در آینده از آن حرف خواهم زد.

*1- تیم های قهرمان شش فصل اخیر جام حذفی فوتبال ایران را مجموعه C و تیم های نایب قهرمان همان شش فصل را مجموعه R بنامید؛ اشتراک دو مجموعه و مجموعه C-R را تشکیل دهید.

*2- نمودار ون مجموعه زیر را رسم کنید:

(2)

$\large A \bigtriangleup B = (A\cup B) – (A\cap B) $

به مجموعه بالا، مجموعه تفاضل متقارن A و B گویند.