یک فصل دیگر و مبحثی جذاب. در بیست و پنجمین فصل، به مجموعه مرجع و مفهوم جالب متمم یک مجموعه خواهیم پرداخت.

1-25 مجموعه مرجع

نویسنده ای خوشفکر در داستان کوتاهی چنین آورده که “کتابخانه ای وجود دارد که در آن همه کتاب هایی که انسان می تواند با حروف، نمادها، کلمات و جملات مختلف بنویسد را می توان یافت” در نتیجه تمامی کتاب هایی که تا به امروز نوشته شده یا در آینده نوشته خواهد شد؛ در این کتابخانه موجود است(هرچند که اکثریت کتب این کتابخانه گنگ و بی معنا هستند). بدین ترتیب هر مجموعه از کتاب ها (یعنی هرکتابخانه دیگر) زیرمجموعه این کتابخانه خواهد بود. این همان چیزی است که به عنوان مجموعه مرجع می خواهیم.

مجموعه مرجع یعنی تمامی مجموعه های مورد بحث، زیرمجموعه آن مجموعه باشند. آیا این مجموعه لزوما نامتناهی است؟ خیر. وقتی که ما در مورد اعداد یک رقمی مثبت صحبت می کنیم؛ مجموعه مرجع یک مجموعه 9 عضوی است. در اینجا علاقه دارم هر مجموعه مرجع را با U نشان دهم. اگر هنوز درک نکردید که مجموعه مرجع چیست، این را در نظر بگیرید که این مجموعه دشمن تهی است. تهی هیچ عضوی نداشت ولی این مجموعه همه اعضای مورد بحث را شامل می شود.

2-25 مجموعه متمم

همان چیزی که در مورد دشمنی مجموعه مرجع با مجموعه تهی گفتم را می توان به دیگر مجموعه ها تعمیم داد. مجموعه دلخواه A را در نظر بگیرید؛ مجموعه ای دشمن A است که شامل اعضایی از U باشد که در A نباشد. این همان تعریف $U-A$ است. پس متمم A را که با $A’$ نمایش می دهیم به صورت زیر است:

(1)

$\large A’=U-A$

از تعریف متمم دو عبارت مهم زیر به سادگی بدست می آید:

(2)

$\large A \cup A’ = U $

(3)

$ \large A \cap A’ = \varnothing $

طبق تعریف متمم، تهی متمم مجموعه مرجع است (چیزی شبیه صفر شدن هرعدد منهای خودش):

(4)

$\large \varnothing=U-U $

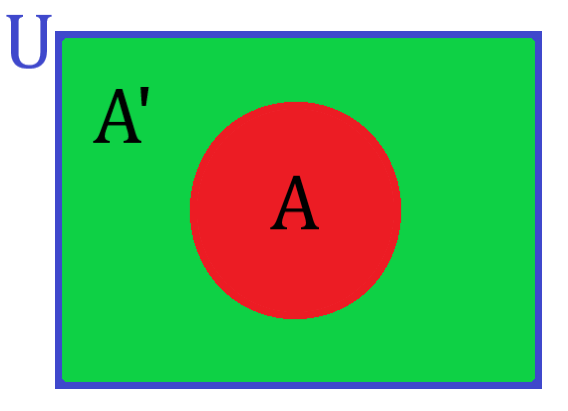
شکل 25-1، مجموعه $A$ با رنگ قرمز، مجموعه $A’$ با رنگ سبز و مجموعه مرجع $U$ با رنگ آبی مشخص شده است.

در 24-2، گفتم بیانی اشتراکی برای $A-B$ وجود دارد. $A-B$ شامل اعضایی است که در A باشند و در B نباشند. چه اعضایی حتما در B نیستند؟ اعضایی که عضو متمم B باشند. پس $A-B$ همان اشتراک A و متمم B است:

(5)

$\large A-B=A \cap B’ $

3-25 جمع بندی فصل

در این فصل با مجموعه مرجع و متمم یک مجموعه آشنا شدیم. همچنین بیان دیگری از تفاضل دو مجموعه را بوسیله مجموعه متمم دیدیم که در برخی مسائل مربوط به جبر مجموعه ها راهگشا است.

*1- مجموعه مرجع U را اعداد صحیح بزرگتر از 1 در نظر بگیرید. دو مجموعه نامتناهی مثال بزنید که متمم یکدیگر باشند.

*2- در شرایط زیر $A’ \cap B $ و $ A\cup B’$ را بیابید؛ سپس اجتماع و اشتراک این دو مجموعه را محاسبه کنید:

$\large U=\{1,2,3,4,5,6\}$ $\large ,A=\{1,2\}$ $\large ,B’=\{1,5,6\}$