اتساع شاید واژه سنگینی باشد. این واژه در اصل یعنی کشیدگی که یعنی زمان کش می آید یا کند می شود. این واقعه از دیدگاه ذهن ما تعجب آور است که اختلاف زمانی دو رویداد، از نظر دو ناظر می تواند متفاوت باشد. با این حال نسبیت خاص و تبدیلات حاکم بر آن یعنی تبدیل لورنتس از چنین چیزی پشتیبانی می کند.
1-11 اتساع با تبدیل لورنتس
مطابق معمول دو چارچوب لخت $S$ و $S’$ را در پیکربندی استاندارد فرض می کنیم. ناظر $S$ ساعتی به دست گرفته و از رویداد $A$ به رویداد $B$ می رسد. به این ترتیب، چون خود چارچوب بر این ساعت واقع شده، اختلاف مکانی میان دو رویداد $A$ و $B$ در ناظر $S$ وجود ندارد $\Delta x=0$ . با توجه به تبدیل لورنتس خواهیم داشت:
$\begin{equation} \Delta t’=\gamma \Delta t \tag{11.1} \label{eq:11.1} \end{equation}$
که با فرض $c=1$ در آن عامل لورنتس $\gamma = \displaystyle{\frac{1}{\sqrt{1-v^2}}}$ است. به این ترتیب زمان برای ساعتی که با سرعت یکنواخت نسبت به $S$ حرکت می کند و ساعتی که نسبت به آن ساکن است (ساعت همراه) متفاوت است و اولی نسبت به دومی با یک ضریب $\gamma$ (که همواره از یک بیشتر است) کش می آید و کندتر کار می کند $\Delta t’ > \Delta t$ .
آهنگ تغییر زمان برای ساعت همراه بیشترین مقدار است درحالیکه برای حرکت با سرعتی نزدیک به $c$، آهنگ به صفر نزدیک می شود، انگار که تیک ساعت های با سرعت بالا نسبت به $S$ بسیار کند باشد. نکته جالب اینکه این ساعت می تواند هرچیزی باشد که به بازه زمانی مربوط است. افرادی که از شما با سرعت یکنواخت دور می شوند (از دید شما) جوانتر می مانند.
**مثال 11-1 |
|
میون ها ذرات ناپایداری اند که از در لایه های فوقانی جو (حدود $10$ کیلومتر بالاتر از سطح زمین) در اثر برخورد پرتوهای کیهانی با مولکول های حاضر ایجاد می شوند. نیم عمر میون $\tau = 2.2 \: \mu s$ است و این ذرات سرعتی در حدود $v=0.998c$ دارند. تعداد زیادی از این ذرات توسط آشکارسازهای سطح زمین رویت می شوند: الف) بدون درنظر گرفتن نسبیت، میون با طی حدودا چه مسافتی نابود می شود؟ معیار نابودی را طی زمان نیم عمر در نظر بگیرید. ب) این بار مسئله مسافت را با در نظر گرفتن اتساع زمان حل کنید. |
پاسخالف) مسافت به صورت زیر محاسبه می شود: $\begin{equation} d = v \tau = (0.998 \times 3 \times 10^8 \: m/s) (2.2 \times 10^{-6} \: s)= 659 \: m \tag{11.2} \label{eq:11.2} \end{equation}$ بنابراین دیدگاه فیزیک کلاسیک بر این مبنا است که نباید تعداد قابل توجهی میون با توجه به فاصله $10$ کیلومتری به سطح زمین برسد. ب) در دیدگاه نسبیتی، از نگاه ناظر زمین، زمان برای میون ها کشیده می شود: $\begin{equation} \tau’=\gamma \tau = \displaystyle{\frac{1}{\sqrt{1-0.998^2}}} (2.2\: \mu s) = 34.8 \: \mu s\tag{11.3} \label{eq:11.3} \end{equation}$ حال محاسبه مسافت مانند مورد الف امکان پذیر است: $\begin{equation} d’ = v \tau’ = (0.998 \times 3 \times 10^8 \: m/s) (34.8 \times 10^{-6} \: s)= 10419 \: m \tag{11.4} \label{eq:11.4} \end{equation}$ بنابراین با درنظر گرفتن اتساع زمان و نسبیت خاص، میون ها می توانند به آشکارساز سطح زمین برسند. با توجه به اینکه زمان مطلقی نداریم، نیم عمر مطلقی هم نداریم. نیم عمر $\tau = 2.2 \: \mu s$ در چارچوب همراه میون است. |
2-11 تقارن اتساع زمان
در نسبیت خاص ناظر مرجحی نداریم. بنابراین هر ناظری می تواند ساعت همراهی داشته باشد و به ساعت دیگران نگاه کند. او مطابق رابطه ($\ref{eq:11.1}$) درمی یابد که در هر بازه زمانی ساعت خودش، بازه زمانی ساعت های دیگر کشیده می شود. به عنوان مثال دو برادر دوقلو، مادامی که با سرعت ثابت نسبت به یکدیگر حرکت کنند؛ هر برادر تصور می کند برادر دیگر جوانتر مانده چون ساعت های او را کندتر می بیند.
3-11 قطار اینشتین
قطار اینشتین آزمایشی ذهنی است که به وسیله آن می توان رابطه اتساع زمان را به شکلی هندسی حساب کرد. در این آزمایش، دو ناظر داریم که یکی در قطاری است که با سرعت $v$ حرکت می کند (ناظر $S$) و دیگری روی سکو خارج قطار ایستاده (ناظر $S’$) است. ناظر داخل قطار، مشاهده می کند که باریکه نوری از آینه کف قطار به سمت آینه سقف آن که دقیقا در یک راستا عمود بر مسیر حرکت قطارند؛ ارسال می شود. فاصله عمودی بین دو آینه از رابطه زیر بدست می آید:
$\begin{equation} L =c \Delta t \tag{11.5} \label{eq:11.5} \end{equation}$
ناظر روی سکو، با توجه به حرکت قطار در می یابد که نور مسیری مورب را طی می کند. به طوری که از لحظه شروع حرکت نور از آینه کف به آینه سقف، قطار مسیری به اندازه $v \Delta t’$ را طی کرده است:
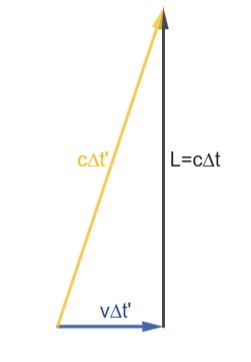
شکل 11-1، دیدگاه ناظر روی سکو؛ مسیر حرکت نور با رنگ طلایی، مسیر حرکت قطار با رنگ آبی و فاصله عمودی میان دو آینه با رنگ خاکستری نمایش داده شده است.
به این ترتیب می توان با استفاده از قضیه فیثاغورث نوشت:
$\begin{equation} c^2 \Delta t^2 + v^2 \Delta t’^2 = c^2 \Delta t’^2\tag{11.6} \label{eq:11.6} \end{equation}$
که با اندکی محاسبه می توان به رابطه ($\ref{eq:11.1}$) رسید.
4-11 زمان ویژه
زمان ویژه یا زمان همراه، زمانی است که توسط ساعتی همراه با ناظر یا جسمی است که از یک رویداد به رویداد دیگر می رسد و از دیدگاه این ناظر خاص، اختلاف مکانی وجود ندارد. این زمان در بخش 11-1، همان $\Delta t$ اندازه گیری شده توسط ناظر $S$ است. معمولا زمان ویژه را با $\tau$ نمایش می دهیم. دلیل اصلی ویژه بودن این زمان، تجربه این دو رویداد در یک مکان است. این مهم نتیجه می دهد که زمان ویژه با ضریبی منفی همان طول فضازمانی ناوردا است $c=1$:
$\begin{equation} \Delta s^2 = – \Delta \tau ^2 \tag{11.7} \label{eq:11.7} \end{equation}$
زیرا $\Delta x = \Delta y = \Delta z = 0$. بنابراین زمان ویژه نیز کمیتی ناورداست. رابطه ($\ref{eq:11.1}$) به شکل دیفرانسیلی نیز حائز اهمیت است:
$\begin{equation} d \tau=\frac{1}{\gamma} d t’ \tag{11.8} \label{eq:11.8} \end{equation}$
تمرینات |
| **1- دو برادر دوقلو تا 30 سالگی در کنار هم زندگی می کنند. پس از آن برادر دوم با سرعت 0.5 سرعت نور نسبت به برادر اول، از او دور می شود. پس از گذشت 30 سال دیگر، از دید برادر اول، برادر دوم چند ساله است؟
**2- در سوال 1، هنگامی که برادر دوم پی میبرد برادر اول 60 ساله است، خودش چند سال سن دارد؟ |




