نمودار مینکوفسکی ابزار هندسی برای توصیف و حل مسائل نسبیت است. همانطور که پیش تر بحث کردیم؛ برای راحتی در دستگاه یکایی قرار می گیریم که $c=1$ باشد. به این صورت می خواهیم نموداری طراحی کنیم که محور عمودی آن $t$ و محور افقی آن $x$ باشد. چنین نموداری به یک بعد فضایی بالاتر نیز قابل تعمیم است و گاها از آن نیز استفاده می کنیم.

1-10 ناظر (چارچوب) های مختلف

ناظر $S$ را در نظر بگیرید با مختصات $(t,x)$، محورهای قائم را تشکیل می دهند. محور مکانی و زمانی ناظرهای دلخواه دیگر مانند $S’$ یا $S^{”}$ را می توان به شکل محورهایی منحرف شده از دو محور قائم نمایش داد. البته بازهم قابل ذکر است که مبداء تمامی ناظرها را یکسان فرض می کنیم. تبدیل لورنتس معادله این محورها را توصیف می کند. محور $t’$ رابطه $x’=0$ و محور $x’$ رابطه $t’=0$ را توصیف می کند. از تبدیل لورنتس داریم:

$\begin{equation} \displaylines{ x’=\gamma (x-vt) \\ t’= \gamma(t-vx) } \tag{10.1} \label{eq:10.1} \end{equation}$

که در آن عامل لورنتس $\gamma = \displaystyle{\frac{1}{\sqrt{1-v^2}}}$ است و چون $c=1$ در نظر گرفتیم $0\le |v| < 1$ . بدین ترتیب محورها از تساوی دو رابطه ($\ref{eq:10.1}$) با صفر بدست می آید:

$\begin{equation} \displaylines{t’: x’=0 \rightarrow x=vt \\ x’: t’=0 \rightarrow t=vx } \tag{10.2} \label{eq:10.2} \end{equation}$

با تنها کردن $t$ به عنوان محور عمودی نمودار:

$\begin{equation} \displaylines{t’: x’=0 \rightarrow t=\frac{1}{v}x \\ x’: t’=0 \rightarrow t=vx } \tag{10.3} \label{eq:10.3} \end{equation}$

به این صورت می توان به راحتی نمودار مینکوفسکی را به تصویر کشید.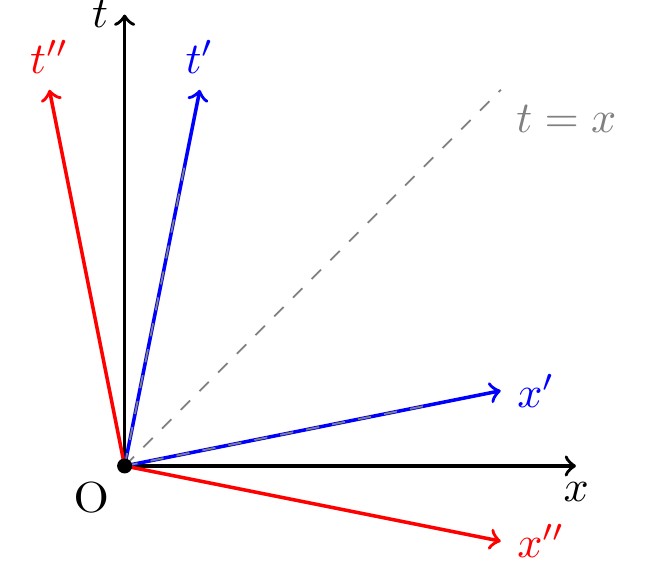

شکل 10-1، نمودار مینکوفسکی سه ناظر، ناظر $S’:(t’,x’)$ سرعتی $0<v<1$ نسبت به ناظر $S$ و ناظر $S^{”}$ سرعتی $-1<v<0$ نسبت به ناظر $S$ داراست. از آن جایی که سرعت نور در همه دستگاه ها یکسان است؛ در هر ناظر $t=x$ ، $t=-x$ و خطوط موازی آن مسیر نور در فضا-زمان را نشان می دهد.

2-10 خطوط همزمانی و هم مکانی

مشابه مختصات دکارتی، خطوط موازی با محور $t’$، خطوطی اند که تمامی رویدادهای آن مکان یکسانی دارند و هم مکان درنظر گرفته می شوند. خطوط  موازی با محور $x’$ نیز رویدادهای آن زمان یکسان دارند و همزمان محسوب می شوند. به این ترتیب مختصه مکانی و زمانی رویداد خاص $A$، در چارچوب $S’$ با خط هم مکانی و خط همزمانی که در تقاطع آن دو واقع شده مشخص می شود.

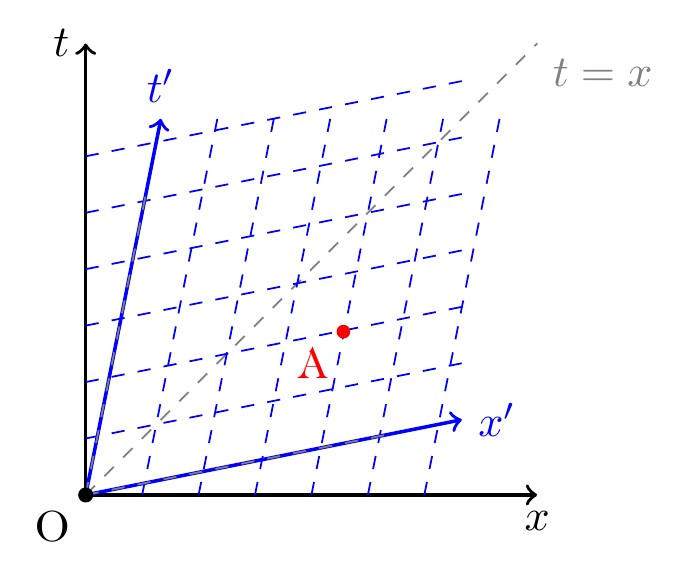
شکل 10-2، خطوط موازی محور مکانی، خطوط همزمانی (مثلا $t’=1,2,3,…$) و خطوط موازی محور زمانی، خطوط هم مکانی (مثلا $x’=1,2,3,…$) است. مختصات رویداد $A$ در هر ناظر به وسیله تبدیل لورنتس قابل تبدیل است.

باید دقت کنیم که در تبدیل مقادیر روی محور های متعامد و غیرمتعامد دیگر قضیه فیثاغورث برقرار نیست. چون فضا-زمان مینکوفسکی با فضای اقلیدسی متفاوت است. در فضای اقلیدسی کمیت طول $\Delta l^2=\Delta x^2+\Delta y^2+\Delta z^2$ کمیتی ناوردا یا بدون تغییر تحت تبدیلات مختصات است. با این حال، با اضافه شدن مختصه زمانی، در فضا-زمان چهاربعدی مینکوفسکی چنین چیزی برقرار نیست و طول می تواند تحت تبدیل لورنتس تغییر کند.

3-10 طول فضا-زمانی

معادل طول ناوردای اقلیدسی، کمیت طول فضا-زمانی است که به شکل زیر تعریف می شود (اینجا دوباره $c$ را برای درک بهتر با نماد خود ذکر می کنیم):

$\begin{equation} \Delta s^2=-c^2 \Delta t^2 +\Delta x^2+\Delta y^2+\Delta z^2  \tag{10.4} \label{eq:10.4} \end{equation}$

ناوردایی طول بالا را می توان از جایگذاری تبدیل لورنتس اثبات نمود:

$\begin{equation} \displaylines{ -c^2 \Delta t’^2 +\Delta x’^2+\Delta y’^2+\Delta z’^2 = \\ -c^2 \gamma^2 (\frac{v^2}{c^4}\Delta x^2 + \Delta t^2 -2\frac{v}{c^2}\Delta x \Delta t) + \gamma^2 (\Delta x^2 + v^2\Delta t^2 -2v\Delta x \Delta t)  + \Delta y^2 + \Delta z^2 = \\ c^2\Delta t^2 (-\gamma^2+\gamma^2\frac{ v^2}{c^2})+\Delta x^2 (\gamma^2-\gamma^2 \frac{v^2}{c^2})+ \Delta y^2 + \Delta z^2   \tag{10.5} \label{eq:10.5}} \end{equation}$

که در رابطه بالا از تعریف عامل لورنتس داریم $\gamma^2-\gamma^2 \frac{v^2}{c^2}=1$ بنابراین:

$\begin{equation} -c^2 \Delta t’^2 +\Delta x’^2+\Delta y’^2+\Delta z’^2 = -c^2 \Delta t^2 +\Delta x^2+\Delta y^2+\Delta z^2  \tag{10.6} \label{eq:10.6} \end{equation}$

کمیت بالا طول فضا-زمانی است که ناوردا تحت تبدیلات لورنتس می باشد. این کمیت به شکل دیفرانسیلی نیز حائز اهمیت است و المان خط فضای مینکوفسکی نام دارد:

$\begin{equation} d s^2=-c^2 d t^2 +d x^2+d y^2+d z^2  \tag{10.7} \label{eq:10.7} \end{equation}$