پیشتر پی بردیم که دیگر خبری از زمان مطلق در چارچوب نظریه نسبیت خاص نیست. زمان و همزمانی نیز مفهومی نسبی دارند و از چارچوبی به چارچوب دیگر ممکن است دو رویداد همزمان نباشند. به طور کلی همزمانی دو رویداد $A$ و $B$، در ناظر $S$ به صورت زیر قابل تعریف است:

$\begin{equation} t_A = t_B \; , \; \Delta t =0 \tag{9.1} \label{eq:9.1} \end{equation}$

اختلاف مکانی این دو رویداد را در $S$، $\Delta x$ در نظر بگیریم. می خواهیم با تبدیل لورنتس در چارچوب دیگری یعنی $S’$، این دو رویداد همزمان در چارچوب $S$ را بررسی کنیم:

$\begin{equation} \Delta t’ = \gamma \frac{v}{c^2} \Delta x \tag{9.2} \label{eq:9.2} \end{equation}$

بنابراین دو رویداد در ناظر دیگر همزمان نیستند و همزمانی امری نسبی است نه مطلق.

1-9 همزمانی با سه ناظر

می توان ایده همزمانی دو ساعت را می توان به وسیله سه ناظر مطرح کرد. شرایط به این شکل است که سه ناظر، فرهاد، فرزانه و سهراب به طوری که فرزانه دقیقا در میانه راه فرهاد و سهراب ایستاده باشد و هرسه ناظر نسبت به هم ساکن باشند. فرزانه دو پرتوی نور به فرهاد و سهراب می فرستد. هنگامی که علامت نوری توسط هردو دریافت شد؛ فرهاد و سهراب ساعت خود را در زمان خاصی کوک کنند و بدین ترتیب مادامی که فرهاد و سهراب نسبت به هم ساکن باشند؛ ساعت هایی همزمان دارند.

نمودار مینکوفسکی، ابزاری کارامد در تحلیل مسائل نسبیت است. در این نمودار زمان محور عمودی و مکان محور افقی در نظر گرفته می شود به طوری که در یکایی بررسی می کنیم که $c=1$. بنابراین نیمساز ربع اول و سوم و خطوط موازی آن مسیر پرتوهای نور در این فضا-زمان است. سه ناظر ما هرکدام باهم فاصله ای یکسان دارند.

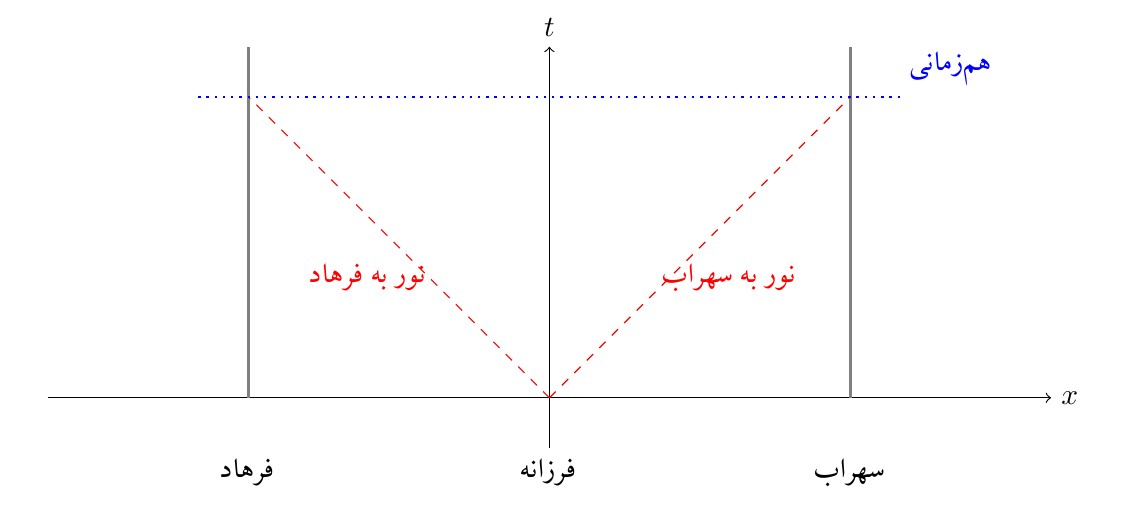
شکل 9-1، فرزانه در مبدا فضا-زمان، دو علامت نوری به فرهاد و سهراب که فاصله یکسانی با هردو دارد می فرستد. فرهاد و سهراب به محض دریافت علامت، ساعت خود را در زمان خاصی کوک می کنند و همزمان می شوند. این همزمانی دو رویداد رسیدن علامت و کوک ساعت تنها از دید فرزانه، سهراب، فرهاد و هر ناظر دیگری است که نسبت به ایشان ساکن باشد.

2-9 همزمانی نسبی است!

در ابتدای فصل، از دیدگاه تبدیل لورنتس پی به نسبی بودن همزمانی در ناظرها بردیم. دو رویداد همزمان در ناظر اول، در ناظر دومی که نسبت به آن با سرعت ثابت حرکت می کند اختلاف زمانی دارد. حال می خواهیم با کمک نمودار مینکوفسکی این مورد را دریابیم. این بار فرض کنید رودابه (ناظر $S’$) با سرعت $-v$ نسبت به سهراب، فرزانه و فرهاد حرکت می کند (یا برعکس که آن ها نسبت به رودابه سرعت $v$ دارند). به طوری که رودابه در مبداء مختصات به فرزانه رسیده و در همان هنگام فرزانه پالس های نوری را به سمت سهراب و فرهاد روانه می سازد. در چنین موقعیتی رویداد رسیدن علامت نوری به فرهاد، زودتر از رویداد رسیدن نور به سهراب توسط رودابه برداشت می شود.

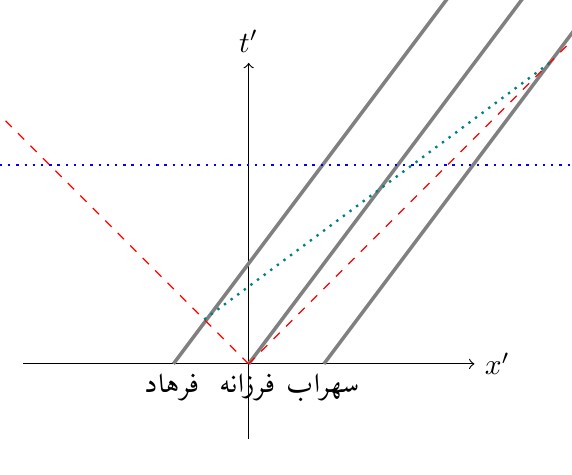
شکل 9-2، مختصات ناظر $S’$ (رودابه) که می بیند سهراب، فرزانه و فرهاد (سه خط خاکستری موازی) به طور متقابل با سرعت $v$ حرکت می کنند. خط آبی خط همزمانی در ناظر $S’$ است که موازی محور $x’$ می باشد. خط سبز خط همزمانی در ناظر $S$ است که دو رویداد رسیدن علامت نوری به فرهاد و سهراب را همزمان نشان می دهد. دو خط قرمز نیز پالس های نوری ارسال شده توسط فرزانه در مبداء مختصات است. رودابه زمان کمتری مطابق نمودار برای رسیدن نور به فرهاد، نسبت به رسیدن نور به سهراب اندازه می گیرد و همزمانی از دیدگاه او موضوعیت ندارد.