در فصول قبل پی بردیم که تبدیلات ساده انگارانه گالیله نمی تواند به درستی اتفاقات فیزیکی درک شده مابین دو ناظر را توصیف کند. تبدیل لورنتس، تبدیلی است جایگزین برای تبدیل گالیله که نحوه تبدیل اندازه گیری های فیزیکی میان دو ناظر یا چارچوب لخت (بدون شتاب) نسبت به یکدیگر را مطابق نسبیت خاص آشکار می سازد.

1-8 شبکه مختصاتی

با این حال می دانیم که زمان در یک چارچوب مختصاتی نسبیتی نقشی کلیدی را ایفا می کند و دیگر خبری از فضا و زمان مطلق نیست. در این حالت به این نیاز داریم که تمامی نقاط دستگاه مختصات چارچوب مان را شبکه بندی کنیم. فرض کنید که در هر نقطه شبکه ذرات آزاد و ساکنی داریم و فواصل نقاط این شبکه بسیار نزدیک و تنظیم شده است. در چنین شرایطی با توجه به اینکه چارچوب ما لخت است، ذرات همواره ساکن می مانند.

حال بر مبدا این شبکه و تمامی ذرات ساعتی نصب می کنیم. در این دستگاه، ساعت روی مبدا در زمان $t_0$ به تمامی نقاط شبکه علامتی نوری می فرستد. چون فاصله هر نقطه شبکه $r$ را از مبدا می دانیم و سرعت نور ثابت است؛ هر ساعت در لحظه $t_0 + r/c$ تنظیم می شود. به این صورت همه ساعت ها همزمان شده و می توان از اختلاف زمان بین رویدادهای فیزیکی مختلف برای این چارچوب سخن گفت.

2-8 تبدیل لورنتس

دو چارچوب لخت دلخواه $S$ و $S’$ را که شبکه مختصاتی در آن ها برقرار شده را درنظر بگیرید. هدف این است که رابطه میان $S$ با مختصات $(t,x,y,z)$ و $S’$ با مختصات $(t’,x’,y’,z’)$ برای رویدادی دلخواه بدست آوریم. اولین گام این است که باید بپذیریم این تبدیل باید خطی باشد. این فرض غیربدیهی نتیجه اصل موضوع معادل بودن چارچوب های لخت است. تنها تحت یک تبدیل خطی، حرکت یکنواخت ذره آزاد در دستگاه $S$ به حرکت یکنواختی دیگر در دستگاه $S’$ منجر می شود. بدین صورت همواره تبدیل ها را (مثلا برای $x’$) می توان به شکل زیر نوشت:

$\begin{equation} x’=Ax+By+Cz+Dt \tag{8.1} \label{eq:8.1} \end{equation} $

که خطی بودن تبدیل ایجاب می کند ضرایب اعدادی ثابت و غیروابسته به مختصات باشند. دیگر ویژگی مهم دو چارچوب این است که $S$ و $S’$ به یکدیگر سرعت هایی برابر ولی با علامت مخالف نسبت می دهند($\pm v$). زیرا مثلا اگر چارچوب $S$ ببیند که $S’$ با سرعت $+v$ به جهت راست (مثلا محور $x$) حرکت می کند؛ به همان شکل $S’$ می بیند که چارچوب $S$ در حال دور شدن با سرعت $-v$ به سمت چپ محور $x$ است که علامت سرعت این جهات را نشان می دهد.

حال در نظر بگیرید که چارچوب $S’$ با سرعت $v$ نسبت به $S$ در جهت محور $x$ حرکت می کنند. با توجه به این که حرکت یکنواخت است و سرعت قرار نیست تغییر کند؛ قرار دادن سرعت در جهت محور $x$ از کلیت مسئله نمی کاهد. همچنین دو چارچوب در پیکربندی استانداردند؛ بنابراین دو صفحه $y=0$ و $y’=0$ که همان صفحه $xz$ و $x’z’$ است برهم منطبق خواهند بود. بنابراین $y’$ تنها می تواند تابعی از $y$ باشد و ضرایب دیگر مختصات صفر خواهد بود زیرا که می تواند هر مقداری اختیاری کند:

$\begin{equation} y’ = A_y y\tag{8.2} \label{eq:8.2} \end{equation} $

در صورتی که علامت چهار محور $x$، $z$، $x’$ و $z’$ را قرینه کنیم. تغییری در واقعیت های فیزیکی مسئله ایجاد نمیشود و صرفا مشابه آن است که یک خیابان را از دو پیاده روی متفاوت می نگریم. بنابراین تبدیل لورنتس باید تحت این تبدیل ناوردا بماند و انگار جای $S$ و $S’$ عوض می شود. پس خواهیم داشت:

$\begin{equation} y = A_y y’ \tag{8.3} \label{eq:8.3} \end{equation} $

که ترکیب ($\ref{eq:8.2}$) و ($\ref{eq:8.3}$) ایجاب می کند که $A_y=\pm 1$. علامت منفی را به این دلیل کنار می گذاریم که در سرعت $v=0$ باید دو محور منطبق باشند. استدلال مشابه روند بالا را می توان برای تقارن صفحه $xy$ نیز انجام داد. بدین صورت دو جزء بدیهی تبدیل لورنتس اثبات می شود:

$\begin{equation} \displaylines{ y’=y \\ z’=z } \tag{8.4} \label{eq:8.4} \end{equation} $

با توجه به اینکه $x’$ ترکیب خطی از مختصات بدون پریم است و همچنین در $x=vt$، مبداء $S’$ یا $x’=0$ را داریم؛ تبدیل باید به صورت زیر باشد:

$\begin{equation} x’=\gamma (x-vt) \tag{8.5} \label{eq:8.5} \end{equation} $

همچنین برای زمان نیز به شکل زیر بسط می دهیم:

$\begin{equation} t’= ax+bt \tag{8.6} \label{eq:8.6} \end{equation} $

این بار مسئله را در مبداء $S$ که $x=0$ یا $x’=-vt’$ است در نظر می گیریم و در روابط ($\ref{eq:8.5}$) و ($\ref{eq:8.6}$) جایگذاری می کنیم:

$\begin{equation} \displaylines{ x’=\gamma (-vt) \\ t’= bt } \tag{8.7} \label{eq:8.7} \end{equation} $

حال دو رابطه ($\ref{eq:8.7}$) را برهم تقسیم می کنیم تا $b$ حاصل شود:

$\begin{equation} \displaystyle{ \frac{x’}{t’}=-v=\frac{-\gamma v}{b}} \tag{8.8} \label{eq:8.8} \end{equation} $

بنابراین از بالا نتیجه می شود که $b=\gamma$. حال دوباره تبدیلات لورنتس را بازنویسی می کنیم:

$\begin{equation} \displaylines{ x’=\gamma (x-vt) \\ t’= \gamma(t-dx) } \tag{8.9} \label{eq:8.9} \end{equation} $

که در ($\ref{eq:8.9}$) صرفا برای سهولت نوشتاری تغییر متغیر $d=\frac{a}{\gamma}$ را لحاظ کرده ایم و می خواهیم آن را بدست آوریم. این بار از حرکت باریکه نور در دو دستگاه کمک می گیریم. سرعت نور مطابق اصل موضوع در همه دستگاه ها یکسان است. بنابراین حرکت باریکه ای نور را به شکل $c=\frac{x’}{t’}=\frac{x}{t}$ در نظر می گیریم (به سادگی مشخص است که می توان تبدیل مکان و زمان را با تبدیل جابجایی های مکانی و زمانی جایگزین کرد؛ مثلا کافی است مثلا تبدیل مکان ثانویه و اولیه را از هم کم کنیم):

$\begin{equation} \displaylines{ ct’=\gamma (c-v)t \\ t’= \gamma(1-dc)t } \tag{8.10} \label{eq:8.10} \end{equation} $

بار دیگر دو رابطه را بر هم قسمت می کنیم:

$\begin{equation} \displaystyle{ c=\frac{c-v}{1-dc}} \tag{8.11} \label{eq:8.11} \end{equation} $

$\begin{equation} c-dc^2=c-v \rightarrow d=\displaystyle{ \frac{v}{c^2}} \tag{8.12} \label{eq:8.12} \end{equation} $

بنابراین شکل نهایی تبدیل لورنتس را بدست آوریم و حالا تنها مجهول ما $\gamma$ است:

$\begin{equation} \displaylines{ x’=\gamma (x-vt) \\ t’= \gamma(t-\frac{v}{c^2}x) } \tag{8.13} \label{eq:8.13} \end{equation} $

برای بدست آوردن $\gamma$ نیاز داریم که معکوس تبدیل را نیز داشته باشیم. قبلا اشاره کردیم که تنها تفاوت برای سرعت از نظر دو چارچوب، علامت آن است یعنی $v \rightarrow -v$ و بقیه ویژگی ها به شکل مشابه تبدیل می شوند:

$\begin{equation} \displaylines{ x=\gamma (x’+vt’) \\ t= \gamma(t’+\frac{v}{c^2}x’) } \tag{8.14} \label{eq:8.14} \end{equation} $

شرایط مهیاست که رابطه ($\ref{eq:8.13}$) را در رابطه اول ($\ref{eq:8.14}$) قرار دهیم:

$\begin{equation} \displaystyle{ x=\gamma (\gamma x -\gamma vt+v(\gamma t – \gamma\frac{v}{c^2}x )) } \tag{8.15} \label{eq:8.15} \end{equation} $

($\ref{eq:8.15}$) را به شکلی مرتب می کنیم که $x$ در یک طرف معادله تنها شود و همچنین $\gamma vt$ و قرینه اش با هم حذف می شوند:

$\begin{equation} \displaystyle{ x(1-\gamma^2+\gamma^2\frac{v^2}{c^2})=0} \tag{8.16} \label{eq:8.16} \end{equation} $

در ($\ref{eq:8.16}$) واضح است که در حالت کلی $x \neq 0$ پس پرانتز برابر با صفر است؛ معادله را حل می کنیم تا به $\gamma$ برسیم:

$\begin{equation} \displaystyle{ \gamma^2(1-\frac{v^2}{c^2})=1} \tag{8.17} \label{eq:8.17} \end{equation} $

بنابراین $\gamma$ به صورت زیر می تواند باشد:

$\begin{equation}  \gamma=\pm\displaystyle{\frac{1}{ \sqrt{ 1-\frac{v^2}{c^2}} } }  \tag{8.18} \label{eq:8.18} \end{equation} $

با این حال جواب منفی قابل قبول نیست؛ زیرا تبدیل لورنتس در سرعت های بسیار پایین باید به تبدیل گالیله تبدیل شود و $\gamma \sim  1$ خواهد بود. به این ضریب $\gamma$، عامل لورنتس می گویند.

 

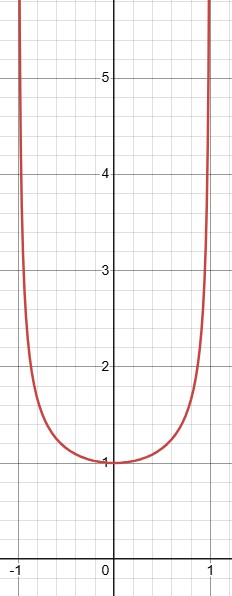
شکل 8-1، نمودار عامل لورنتس $\gamma$ برحسب سرعت بر سرعت نور $v/c$، عامل لورنتس در سرعت های نزدیک به سرعت نور به بی نهایت نزدیک می شود و در سرعت های بسیار پایین به یک. مطلب دوم نشان دهنده این است که حد کلاسیک تبدیل لورنتس، تبدیل گالیله است.

به این ترتیب، تبدیل لورنتس به طور خلاصه به شکل زیر است:

$\begin{equation} \displaylines{ t’= \frac{1}{ \sqrt{ 1-\frac{v^2}{c^2}}}(t-\frac{v}{c^2}x) \\ x’=\frac{1}{ \sqrt{ 1-\frac{v^2}{c^2}}} (x-vt) \\ y’=y \\ z’=z } \tag{8.19} \label{eq:8.19} \end{equation} $

گاها برای ساده نویسی بیشتر در یکایی محاسبات را انجام می دهیم که $c=1$ باشد. شکل تغییرات زمانی و مکانی، همانطور که گفته شد از رابطه بالا به سهولت قابل دستیابی است:

$\begin{equation} \displaylines{ \Delta t’= \frac{1}{ \sqrt{ 1-v^2}}(\Delta t-v\Delta x) \\ \Delta x’=\frac{1}{ \sqrt{ 1-v^2}} (\Delta x-v\Delta t) \\ \Delta y’=\Delta y \\ \Delta z’=\Delta z } \tag{8.20} \label{eq:8.20} \end{equation} $

 

تمرینات

*1- ناظر $S’$ با سرعت $0.8$ سرعت نور نسبت به ناظر $S$ در جهت محور $x$ حرکت می کند؛ اگر ناظر $S$ فاصله زمانی و مکانی دو رویداد را به ترتیب $5$ ثانیه و $100$ متر اندازه گیری کند. ناظر $S’$ فاصله زمانی و مکانی را چقدر اندازه می گیرد؟ **2- تحت چه شرایطی ترتیب وقوع زمانی دو رویداد برای دو ناظر تغییر می کند؟ (شرط را به شکل یک نامساوی بدست آورید.)