در مقالات قبلی با تشابه های حرکت انتقالی و حرکت دورانی آشنا شدیم؛ در این مقاله قصد داریم که دو تعریف مهم کار و انرژی جنبشی را برای حرکات دورانی نیز استفاده نماییم.
انرژی جنبشی دورانی
از رابطه مشهور K=mv2/2 برای حرکت دورانی، از کمیت های مشابه مانند لختی دورانی و سرعت زاویه ای استفاده می کنیم، تا انرژی جنبشی یک جسم صلب در حال دوران را تعریف کنیم:
(1)
کار
کار انجام شده توسط گشتاور نیرو در یک بازه خاص جابجایی زاویه ای به طور مشابه با کار انجام شده توسط یک نیرو در یک بازه خاص جابجایی، بصورت زیر تعریف می شود:
(2)
در صورتی که گشتاور نیرو ثابت باشد، رابطه بالا به صورت ساده زیر تبدیل می شود:
(3)
توان
توان نیز که آهنگ انجام دادن کار (مشتق زمانی کار) است، در دوران حول یک محور ثابت به صورت زیر تعریف می شود:
(4)
قضیه کار- انرژی جنبشی در حرکت دورانی
از پایستگی انرژی پی می بریم که انجام شدن کار روی جسمی صلب که حول محوری ثابت در حال دوران است؛ باعث تغییر در انرژی جنبشی دورانی جسم شود. حال قضیه معروف کار-انرژی جنبشی در حرکت دورانی نیز تعریف می شود:
(5)
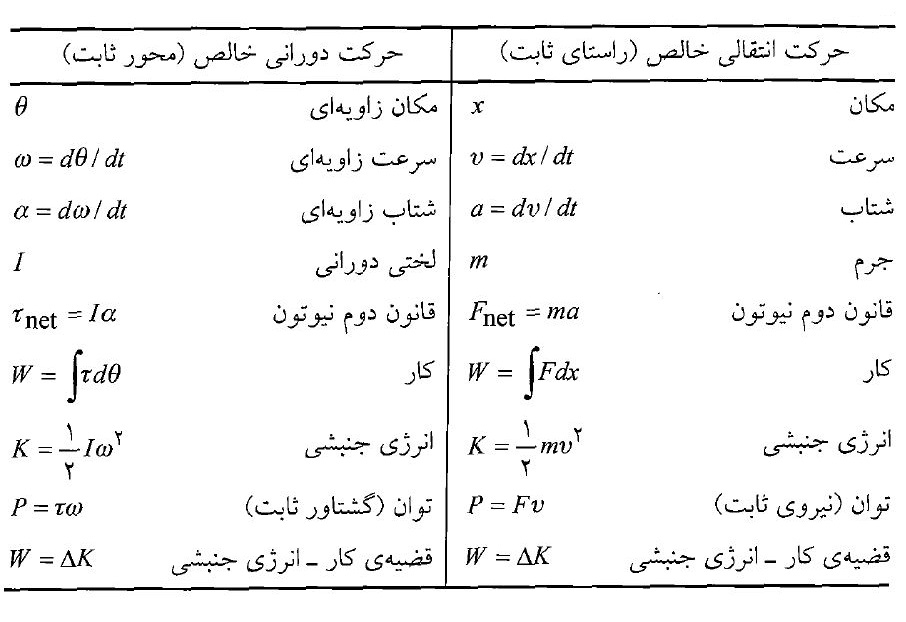
جدول زیر نشان دهنده برخی روابط متناظر در حرکت انتقالی و دورانی است:
*تمرین حل شده)
گشتاور نیرویی بر روی صفحه ای مستطیلی ساکن به جرم 12 کیلوگرم، طول 2 متر و عرض یک متر، حول محور عمود گذرنده از مرکز، 5 ژول کار انجام می دهد؛ بزرگی سرعت زاویه ای جسم پس از پایان انجام کار روی صفحه چقدر است؟ (از اصطکاک صرف نظر کنید)
با توجه به جدول مقاله انرژی جنبشی دورانی و لختی دورانی، لختی دورانی صفحه را محاسبه می نماییم:
حال از رابطه کار-انرژی جنبشی دورانی برای محاسبه سرعت زاویه ای بهره می بریم:

مسائل بیشتری می خواهید؟
بزودی


