مخروط زمانی یا مخروط نوری یک رویداد، رویدادهایی را نشان می دهد که می توانند در گذشته یا آینده آن رویداد قرار گیرند. برای پی بردن به خواص این مخروط باید با علیت رویدادهای نسبیتی آشنا شویم.

1-13 ترتیب علّی رویدادهای نسبیتی

دو رویداد دلخواه $A$ و $B$ را در فضازمان در نظر بگیرید. این دو رویداد تنها در صورتی می توانند با هم به طور علی مربوط باشند که یک شیء بتواند آن دو را با سرعتی حداکثر به اندازه سرعت نور به یکدیگر مرتبط کند $v\le c$ . در چارچوب دلخواه $S$، فاصله مکانی دو رویداد را $\Delta x$ و فاصله زمانی را $\Delta t$ در نظر بگیرید. به این ترتیب سرعت ذکر شده باید $v=\frac{\Delta x}{\Delta t}$ باشد. کمیت ناوردای لورنتسی که می شناسیم بازه یا طول فضازمانی $\Delta s$ است. بنابراین علی القاعده به آن رجوع می کنیم تا از علی بودن دو رویداد در همه چارچوب ها اطمینان حاصل کنیم:

$\begin{equation} \Delta s^2 = – c^2 \Delta t^2 + \Delta x^2 = – c^2 \Delta t^2 + v^2 \Delta t^2 \tag{13.1} \label{eq:13.1} \end{equation}$

در صورت برقراری شرط $v < c$، مربع بازه فضازمانی قطعا منفی خواهد بود $\Delta s^2 < 0$. به این نوع رویدادها، رویداد های زمان گونه می گویند. رابطه علی بین این رویدادها می تواند برقرار باشد. از این جهت به این رویدادها زمان گونه گفته می شود که چارچوبی (چارچوب همراه با شیء توصیف شده که سرعت $v$ دارد) وجود دارد که صرفا با انتقال در زمان و بدون انتقال مکانی از رویداد اول به رویداد دوم می رسد.

اگر $v=c$ باشد نیز رابطه علی امکان پذیر است اما آن شیء تنها موجی است که با سرعت نور منتقل شود مثل یک لیزر. به این رویدادها، رویدادهای نورگونه می گویند. بازه فضازمانی در چنین رویدادهایی صفر است $\Delta s^2 = 0$.

به طور کلی رویدادهایی نمی توانند رابطه علی داشته باشند که نتوان اتصالی مابین آن ها به شکلی که بالا توصیف شد ایجاد کرد. طبیعتا تنها شرط باقی مانده، شرط غیرفیزیکی $v>c$ است که باعث می شود $\Delta s^2 >0$. این دسته رویدادها، رویدادهای فضاگونه اند. برای این دسته از رویدادها، همواره دو چارچوب لخت متمایز وجود دارد که می تواند ترتیب وقوع آن ها را متفاوت با دیگری درک کند.

2-13 مخروط زمانی

تمامی نتایج قبل به سه بعد نیز با جایگزینی $\Delta r$ (فاصله فضایی) به جای $\Delta x$ قابل تعمیم است. حال می توان مکان هندسی مخروط زمانی را بدست آورد. برای هر رویداد دلخواه $O$، تنها رویدادهایی در مخروط زمانی آن هستند که بتوانند با آن رابطه علی داشته باشند حال چه در گذشته چه در آینده رویداد. بدین ترتیب باید $\Delta s^2 \le 0$ برقرار باشد. اگر رویداد $O$ را مبداء مختصات خود در نظر بگیریم؛ مخروط با در نظر گرفتن $c=1$ رابطه زیر را خواهد داشت:

$\begin{equation} – t^2 + r^2 \le 0 \tag{13.2} \label{eq:13.2} \end{equation}$

چهار بعد فضازمانی را در نمودار مینکوفسکی نمی توان به تصویر کشید. اما شکل 13-1 و شکل 13-2، نمایانگر مخروط زمانی رویداد $O$ با دو بعد و سه بعد فضازمانی است.

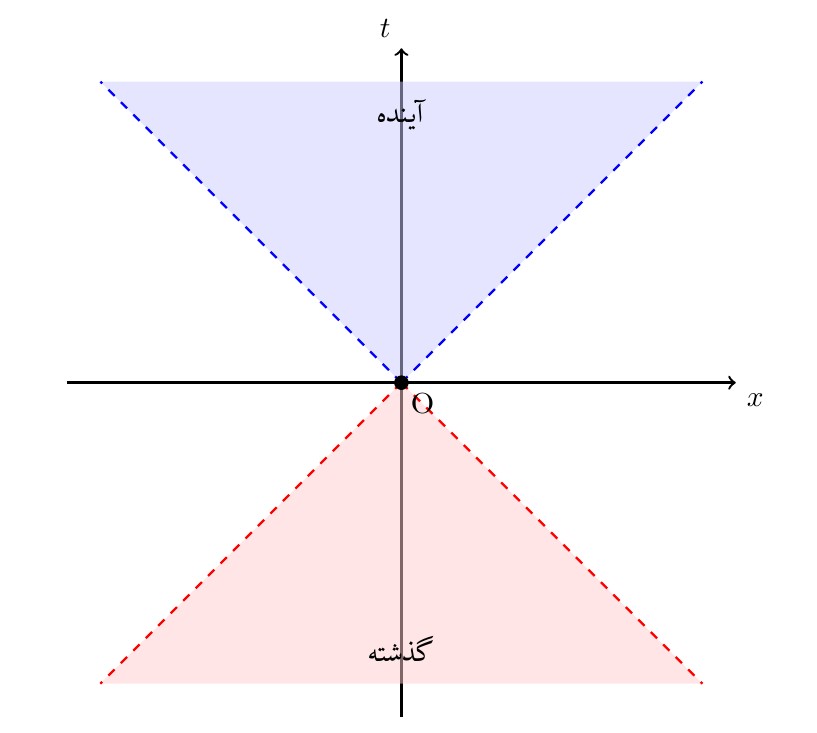
شکل 13-1، نمودار مینکوفسکی دو بعدی مخروط زمانی

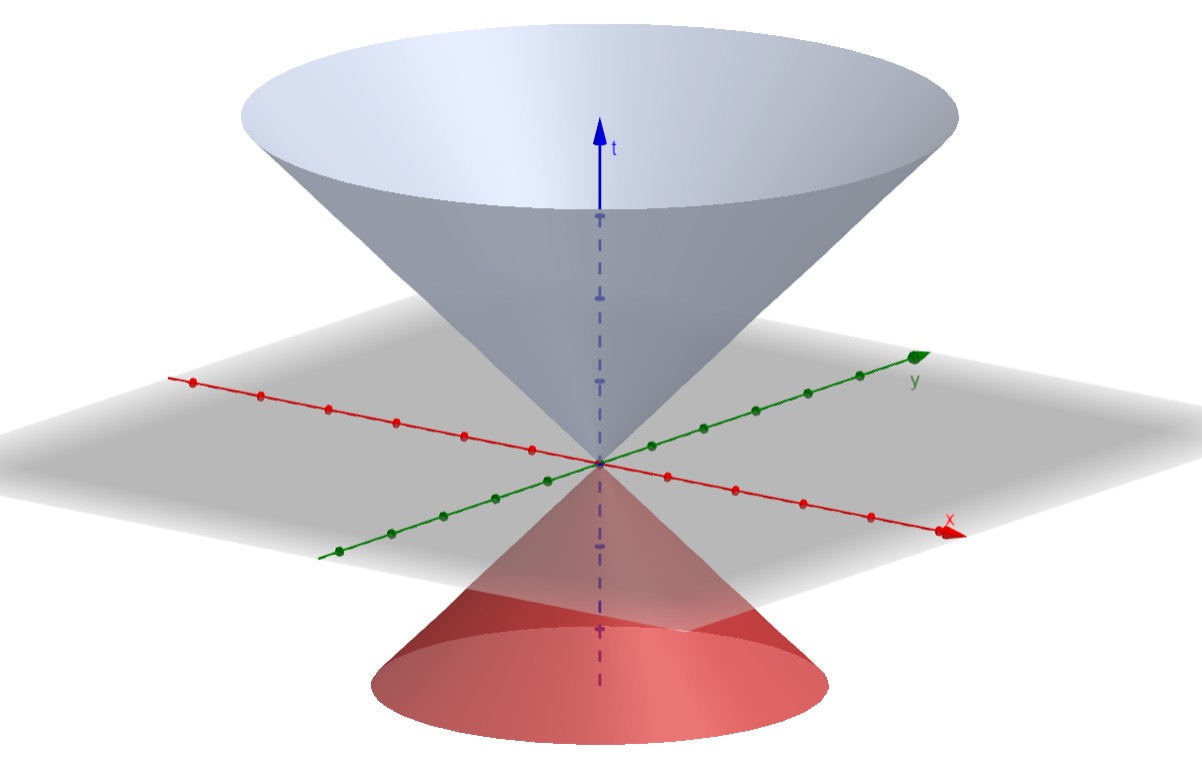
 شکل 13-2، نمودار مینکوفسکی سه بعدی مخروط زمانی