محاسبه احتمال، امکان اندازه گیری شانس وقوع رخدادهای مختلف را برای ما میسر می کند. به عنوان مثال می توان احتمال برنده شدن در قرعه کشی، گردونه شانس یا آمدن تاس مورد نظر را به وسیله کسرها نمایش داد. از کسرها همیشه می توان برای نشان دادن سهم جزئی از کل بهره برد. مثلا روز سه شنبه یکی از هفت روز هفته است، بنابراین $\frac{1}{7}$ کسری است که مدت زمان سه شنبه را به نسبت مدت زمان کل هفته نشان می دهد.
کسرها از سه بخش تشکیل می شوند $\frac{a}{b}$. $a$ صورت کسر نام دارد و $b$ مخرج کسر است و این دو به وسیله یک خط کسری از هم جدا می شوند.
شکل 7-1، کیک شش تکه
شکل کیک بالا را ببینید؛ این کیک به شش تکه مساوی تقسیم شده است. یک تکه از شش تکه کیک را می توان به این صورت نشان داد $\frac{1}{6}$. حال اگر نیمی از کیک را بخواهیم میل کنیم می شود سه تکه که معادل با $\frac{3}{6}$.
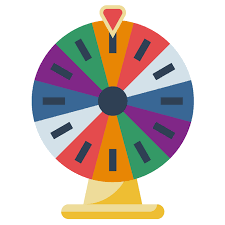
شکل 7-2، گردونه شانس
حال که با کسرها آشنا شدیم می توان احتمال را نیز مورد بررسی قرار داد. همانطور که ذکر شد، کسر ابزار کارآمدی برای نشان دادن احتمالات است. یک گردونه شانس مطابق شکل 7-2 را در نظر بگیرید که با چرخاندن صفحه و ایستادن آن در خانه مدنظر که زیر نشانک گردونه قرار گرفته جایزه می دهد. فرض کنید که گردونه تنها در ناحیه های آبی و بنفش جایزه دارد؛ حال احتمال بردن جایزه چقدر خواهد بود؟ با توجه به اینکه گردونه $12$ ناحیه مساوی دارد؛ هرگاه نشانک در دو بخش بنفش و آبی که $4$ بخش می باشد قرار گیرد برنده می شویم. بنابراین احتمال به صورت $\frac{4}{12}$ نشان داده می شود.
تمرینات |
| *1- در یک کیسه 3 مهره آبی، 2 مهره قرمز و 4 مهره سبز داریم. اگر از داخل کیسه یک مهره خارج کنیم به چه احتمالی این مهره قرمز خواهد بود؟
*2- فرض کنید از کیسه تمرین 1، دو مهره خارج کردیم که یکی سبز و دیگری آبی است؛ حال اگر مهره سومی را خارج کنیم به چه احتمالی قرمز است؟
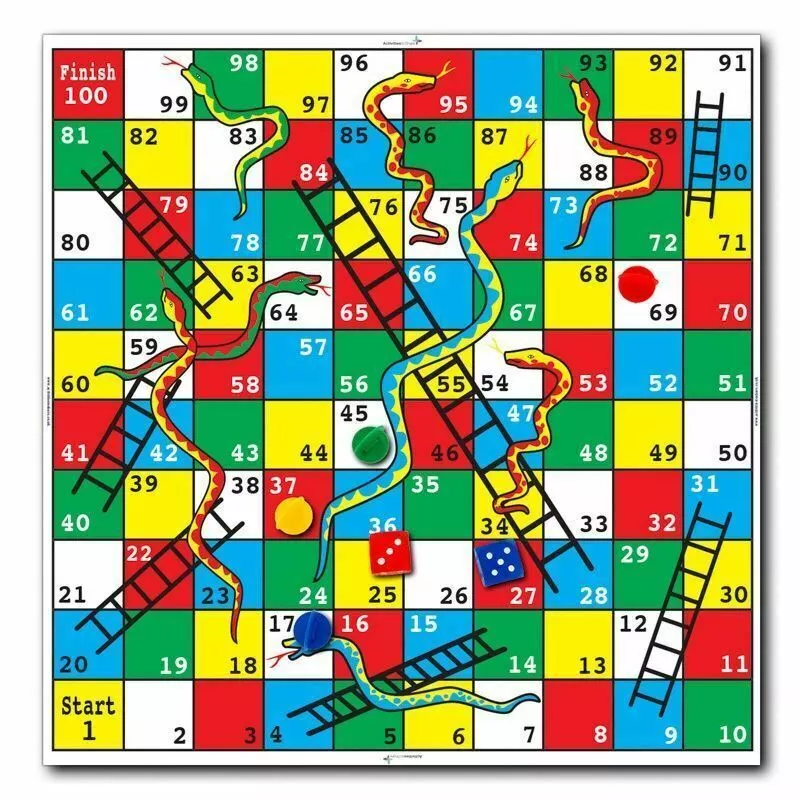
شکل 7-3، بازی مار و پله *3- در بازی مار و پله 100 خانه ای، مهره مهران در خانه 97 قرار گرفته است. او برای حرکت دادن مهره خود باید تاس بیندازد و به اندازه عدد تاس مهره خود را جابه جا کند. در صورتی که تاس او چند بیاید می تواند مهره خود را تکان دهد؟ با چه احتمالی او مهره خود را تکان خواهد داد؟ |