دوباره به این مسئله برمی گردیم که فضای مطلق چگونه از دیگر چارچوب های لخت متمایز می شود. در دوران باستان، ارسطو معتقد بود تمامی اجزای جهان ماورای ماه ( او برای زمین و اطراف آن تا ماه و ماه تا مرزهای جهان تفاوت کیهان شناختی جدی قائل بود.) نظیر ستارگان و… از عنصری سبک تر از هوا و فناناپذیر به نام اتر ساخته شدند؛ زیرا خلا را ناممکن می دانست. با این حال این اتر با اتر مدرن تفاوت های کاملا بنیادی دارد. اندیشمدان قرن هفدهمی همچون دکارت و رابرت بویل، نخستین کسانی بودند که اتر را به عنوان ماده ای پرکننده فضا برای وساطت در انجام کنش های فیزیکی نظیر مغناطیس و… به فیزیک مدرن عرضه داشتند.

نیوتن نیز برای توجیه پدیده هایی همچون پراش نور ،گرانش و انتقال گرما، حدس میزد که یک محیط اتری سبب این افعال فیزیکی می شود. برای معاصران نیوتن، مانند هوک و هویگنس، وظیفه‌ی اصلی اتر، انتقال موج‌های نوری بود. بنابراین آنها حتی اعتقاد به امکان اثر فیزیکی بر روی اتر داشتند. در نهایت این ماکسول بود که دو قرن بعد، دوباره مفهوم “اتر درخشان” را برای انتقال امواج الکترومغناطیس خود احیا نمود که می توانست سازوکاری قابل پذیرش و مشابه با فضای مطلق نیوتنی باشد.

در معادلات ماکسول، ثابت $c$ ظاهر می شود که یکای سرعت دارد. همچنین نظریه ماکسول انتقال اختلالات میدان الکترومغناطیس در خلأ (یا امواج الکترومغناطیسی) را با همین سرعت پیش بینی می کرد. مقدار این سرعت در همان زمان، به وسیله آزمایشات الکترومغناطیسی تعیین شده بود. دیگر مسئله این که سرعت نور نیز شناخته شده و همین مقدار را داشت. این دو ماکسول را رهنمون کرد که نور مرئی را موج الکترومغناطیسی بداند. بنابراین ماکسول یک بستر یا حامل برای انتقال امواج الکترومغناطیسی درنظر گرفت که همان ایده قدیمی اتر بود. به نظر منطقی بود که چارچوب اتر ساکن با چارچوب ستارگان ثابت منطبق باشد؛ یعنی با فضای مطلق نیوتنی. بنابراین، به‌نظر می‌رسید که فضای مطلق، دست‌کم از دیدگاه الکترومغناطیسی، از دیگر چارچوب‌های لخت قابل تمایز است.

1-6 مایکلسون و مورلی به دنبال اتر

نظریه ماکسول به طور گسترده ای موفقیت آمیز بود. این باعث که اتر در کانون توجهات مطالعه و بحث فیزیکی در اواخر قرن نوزدهم قرار گیرد. بنابراین بسیاری از آزمایشگران به دنبال شواهدی تجربی مستقیم از وجود اتر بودند. به طور خاص تلاش های گوناگونی صورت گرفت تا سرعت زمین در اتر به هنگام گردش دور خورشید اندازه گیری شود. این اندازه گیری از طریق “باد اتری” یا “رانش اتری” صورت می پذیرفت. باد اتری به این صورت است که مشابه حرکت در هوا و احساس جریان باد توسط دوچرخه سوار، باید جریان بادی بر روی زمین در اثر وجود اتر حس شود.

این آزمایش در سال 1887 انجام شد. مایکلسون و مورلی یک پرتو نور را بوسیله یک جداکننده به دو مسیر عمود بر هم و با طول مساوی تقسیم کردند و سپس پرتوها را با آینه بازتاب دادند تا به نقطه‌ی آغاز بازگردند، و در آنجا نوارهای تداخلی میان پرتوهای بازگشتی ایجاد شد. اگر مولفه باد اتر در امتداد دو مسیر متفاوت بود، باید اختلافی در زمان‌های طی مسیر پدید می‌آمد. (مشابه این پدیده را می توان با مقایسه شناکردن در عرض رودخانه و شنا در جهت رودخانه دریافت.) اما وقتی دستگاه را ۹۰ درجه چرخاندند؛ این اختلاف باید جهت عکس پیدا می‌کرد اما جابجایی مورد انتظار در نوارهای تداخلی رخ نداد.

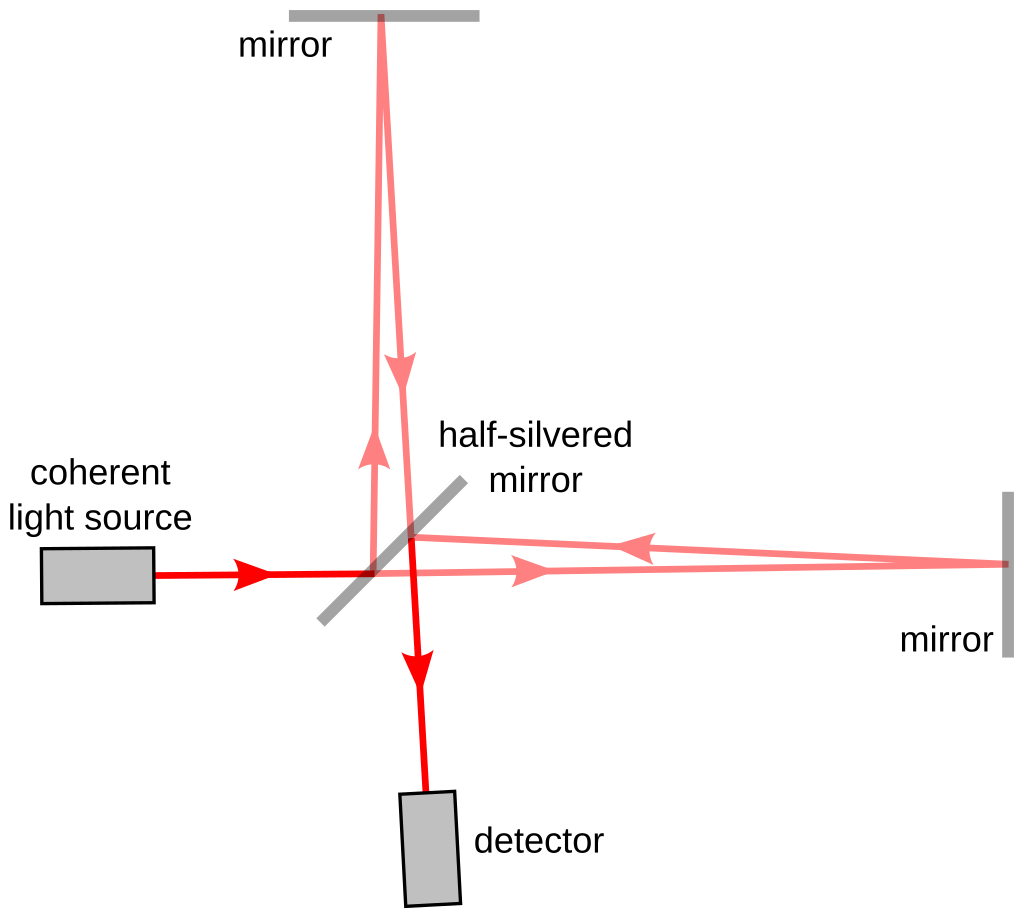
شکل 6-1، طرحی از تداخل سنج مایکلسون. با یک منبع نور همدوس، دو آینه، یک جداکننده پرتو و یک آشکارساز. اختلاف فاز دو موج سبب ایجاد طرح تداخلی می شود.

از آن‌جا که سرعت مداری زمین به دور خورشید برابر با $30 \; km/s$ است، می‌توان انتظار داشت که باد اتری در برخی زمان‌ های سال دستکم به همین مقدار برسد. صرف‌ نظر از اینکه اتر چگونه نسبت به منظومه شمسی جریان دارد. بادی با این اندازه در محدوده توانایی دستگاه برای آشکارسازی قرار داشت. یک توضیح برای عدم مشاهده باد، این بود که زمین اتر را به‌طور کامل در اطراف خود با خود می‌کشاند(انگار که اتر به زمین می چسبد.). چنین توجیهی به دلیل پدیده‌ های نوری دیگر مانند ابیراهی نور ستارگان رد می‌شود. بدین صورت فرض وجود اتر ماکسولی شکننده به نظر می رسید.

2-6 نظریه اتر لورنتس و انقباض لورنتس – فیتزجرالد

در سال 1889 فیتزجرالد و ظاهرا به طور مستقل از او در سال 1892، لورنتس پیشنهاد دادند که طول اجسام در حال حرکت در اتر با سرعت $v$، در جهت حرکتشان، به اندازه ضریب $\sqrt{1-v^2/c^2}$ کوچکتر می شود. این فرضیه سبب جبران اثر باد اتری در آزمایش مایکلسون – مورلی بود و آن را توجیه می نمود.

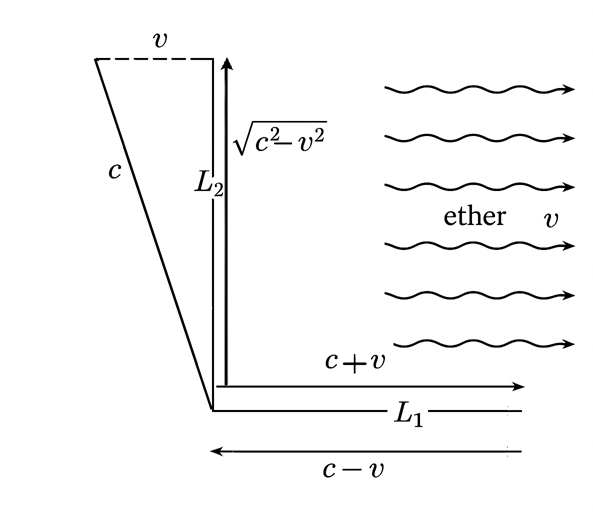
شکل 6-2، دستگاه مایکلسون مورلی با دو بازوی $L_1$ در راستای سرعت $v$ و بازوی $L_2$ عمود بر راستای سرعت $v$.

می خواهیم ببینیم که “انقباض لورنتس – فیتزجرالد” چگونه کار می کند. فرض کنید یکی از بازوهای دستگاه مایکلسون – مورلی به طول $L_1$ در راستای باد اتر و دیگری به طول $L_2$ عمود بر آن است. برای بازوی $L_1$ نور یکبار در جهت $v$ و بار دیگر، خلاف جهت آن حرکت می کند. بنابراین سرعت نور یکبار ٍ$c+v$ و بار دیگر $c-v$ است. برای بازوی $L_2$ نیز هنگامی که نور از ابتدای بازو به آینه می رسد؛ کل مجموعه با سرعت $v$ جابجا شده است. بنابراین سرعت در جهت این بازو مطابق قضیه فیثاغورث $\sqrt{c^2-v^2}$ است (شکل 6-2). با این توضیحات زمان $T_1$ که زمان رفت و برگشت نور در بازوی $L_1$ است به صورت زیر خواهد بود:

$\begin{equation} \displaystyle{T_{1}=\frac{L_1}{c+v}+\frac{L_1}{c-v}=\frac{2c L_1}{c^2-v^2}=\frac{2L_1}{c(1-v^2/c^2)}}\tag{6.1} \label{eq:6.1} \end{equation}$

به طور مشابه $T_2$ که زمان رفت و برگشت نور در بازوی $L_2$ است:

$\begin{equation} \displaystyle{T_{2}=\frac{2L_2}{\sqrt{c^2-v^2}}=\frac{2L_2}{c(1-v^2/c^2)^{1/2}}}\tag{6.2} \label{eq:6.2} \end{equation}$

ظاهرا طول دو بازوی $L_1$ و $L_2$ برابر است و زمان ها متفاوت. اما اگر انقباض لورنتس – فیتزجرالد را در نظر بگیریم تفاوت زمانی از بین می رود و نتیجه آزمایش توجیه می شود:

$\begin{equation} \displaystyle{L_{1}= \sqrt{1-v^2/c^2} L_{2}}\tag{6.3} \label{eq:6.3} \end{equation}$

از قرار دادن ($\ref{eq:6.3}$) در ($\ref{eq:6.1}$) داریم:

$\begin{equation} \displaystyle{T_{1}=\frac{2\sqrt{1-v^2/c^2} L_{2}}{c(1-v^2/c^2)}=\frac{2L_2}{c(1-v^2/c^2)^{1/2}}=T_{2}}\tag{6.4} \label{eq:6.4} \end{equation}$

نظریه‌ی اتر لورنتس تمام یافته‌ های اولیه نظریه اینشتین را در بر می‌گرفت؛ از نظر محاسباتی معادل با نسبیت خاص بود و با پیش‌فرض‌های کلاسیک کمتر در تضاد قرار می‌گرفت. اما این نظریه از نظر زیبایی‌ شناختی ضعیف تر از نسبیت و مهم‌تر از آن، در ارائه و توجیه نتایج جدید کاملا ناتوان بود. به همین دلیل امروزه تنها مورد توجه مورخان علم قرار دارد.

ّ