51 انتگرال : جزء به جزء

انتگرال گیری جزء به جزء، روشی است که بوسیله آن می توان برخی از انتگرال های حاصل ضرب توابع (که ظاهر دشواری دارند) به سادگی محاسبه کرد. این قاعده، بر مشتق گیری حاصل ضرب استوار است. 1-51 اثبات همانطور که گفتم این روش انتگرال گیری به مشتق گیری حاصل ضرب توابع مربوط است. از فصل […]
50 انتگرال : تابع نمایی و لگاریتمی

در این فصل قصد داریم به انتگرال تابع نمایی و لگاریتمی بپردازیم. مطابق معمول، انتگرال را به چشم پادمشتق می بینیم و با استفاده از مشتق گیری، پی به انتگرال های نامعین مدنظرمان می بریم. رجوع به فصل 46 می تواند در یادگیری این فصل راهگشا باشد. 1-50 تابع نمایی طبیعی می دانیم که مشتق […]
49 انتگرال : توابع مثلثاتی

در بحث مشتق گیری با مشتق روابط مثلثاتی آشنا شدیم. همانطور که دیدیم خود توابع مثلثاتی هستند که عملیات مشتق گیری بر آنها، توابع مثلثاتی تولید می کند. بنابراین انتظار داریم که تابع اولیه برای یک تابع مثلثاتی، بازهم تابعی مثلثاتی باشد. بدون فوت وقت به سراغ معرفی انتگرال توابع مثلثاتی می رویم که بسیار […]
48 انتگرال : چندجمله ای توانی
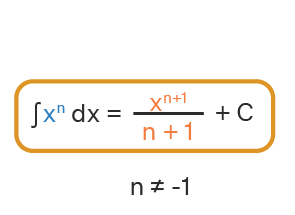
همانطور که در مشتق گیری با چندجمله ای های توانی کار را آغاز کردیم؛ ابتدا بهتر است با نحوه انتگرال گیری از این نوع عبارات آشنا شویم. 1-48 انتگرال عدد ثابت کلید درک و دریافت انواع انتگرال، توجه به مفهوم پادمشتق است. اینکه مشتق چه چیزی یک عدد ثابت همانند $k$ می شود، می دانیم […]
47 انتگرال : مقدمه
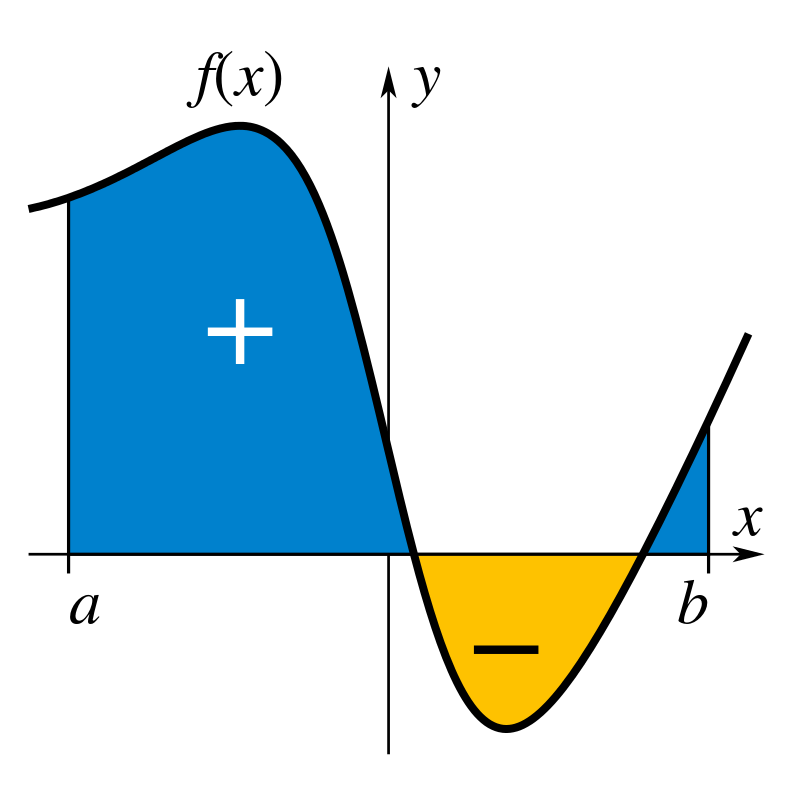
پس از سلسله مباحث مشتق، حالا آماده ایم با مفهوم انتگرال آشنا شویم. انتگرال را می توان از دو دیدگاه بررسی کرد؛ اول اینکه انتگرال را می توان به عنوان عملیاتی معکوس مشتق درک کرد و دوم اینکه بوسیله انتگرال، مقدار مساحت زیر منحنی ها در دستگاه مختصات قابل محاسبه است که به ما در […]
46 مشتق : تابع نمایی و لگاریتمی

در فصول قبل با توابع نمایی و لگاریتمی آشنا شدیم. اکنون زمان آن رسیده که به مشتق آنها بپردازیم. تابع نمایی طبیعی $e^{x}$ یک خاصیت جالب دیگر نیز دارد؛ اینکه مشتق آن برابر با خودش است. برای بدست آوردن مشتقات چنین توابعی ابتدا بهتر است با نمادگذاری کارآمد لایب نیتس آشنا شویم. شکل 46-1، گوتفرید […]
45 مشتق : قاعده هوپیتال

در این فصل، به طریقه ای از محاسبه حدهای مبهم می پردازیم که با مشتق گیری از دو تابع صورت و مخرج صورت می پذیرد. بکارگیری این روش برای نخستین بار به گیوم دو لوپیتال، ریاضی دان فرانسوی نسبت داده می شود. به همین جهت این قاعده را قاعده هوپیتال می نامند. 1-45 اثبات می […]
44 مشتق : قاعده زنجیره ای
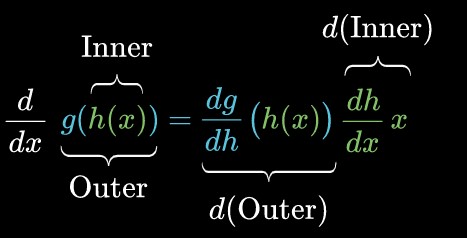
در این فصل، قصد آشنایی با مشتق ترکیب توابع را داریم. ابتدا به این موضوع خواهیم پرداخت که توابع چگونه در یکدیگر ترکیب می شوند و می توان از ترکیب آن ها مشتق گرفت. به این قاعده مشتق گیری، قاعده زنجیره ای می گویند. پس از آن از این نوع مشتق گیری استفاده می کنیم […]
43 مشتق : قاعده ضرب
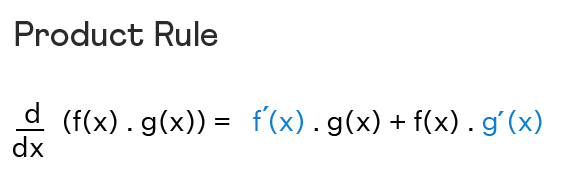
در این فصل به مشتق گیری از دو تابع که در یکدیگر ضرب شده اند؛ می پردازیم. به عنوان مثال، مشتق ضرب یک تابع مثلثاتی در چندجمله ای توان دار می تواند برای ما حائز اهمیت باشد. نتیجه به توابع بیشتر نیز قابل تعمیم خواهد بود. 1-43 قاعده ضرب دو تابع $f$ و $g$ را […]
42 مشتق : توابع مثلثاتی
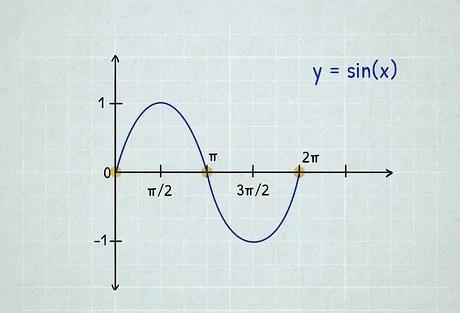
در این فصل به نحوه مشتق گیری از توابع مثلثاتی سینوس و کسینوس می پردازیم. باید در نظر داشت که بسیاری از رفتارهای سامانه های طبیعی به صورت تناوبی است و برخی از کمیت، بوسیله مشتق دیگر کمیات فیزیکی بدست می آید. بنابراین مشتق گیری از توابع مثلثاتی اهمیت بسزایی دارد. 1-42 مشتق سینوس مشتق […]